Product: Abaqus/Standard
The parallel network nonlinear viscoelastic model:
is intended for modeling materials that exhibit nonlinear viscous behavior and undergo large deformations;
consists of multiple elastic and viscoelastic networks in parallel;
uses a hyperelastic material model to specify the elastic response; and
uses multiplicative split of the deformation gradient and a flow rule derived from a creep potential to specify the viscous behavior.
The parallel network nonlinear viscoelastic model consists of multiple elastic and viscoelastic networks connected in parallel, as shown in Figure 22.8.2–1. The number of viscoelastic networks, N, can be arbitrary; however, at most one purely elastic equilibrium network (network 0 in Figure 22.8.2–1) is allowed in the model. If the elastic network is not defined, the stress in the material will relax completely over time.
The model can be used to predict complex behavior of viscous materials subjected to finite strains, which cannot be modeled accurately using the linear viscoelastic model available in Abaqus (see “Time domain viscoelasticity,” Section 22.7.1). An example of such complex behavior is depicted in Figure 22.8.2–2, which shows normalized stress relaxation curves for three different strain levels. This behavior can be modeled accurately using the nonlinear viscoelastic model, but it cannot be captured with the linear model. In the latter case, the three curves would coincide.
The elastic part of the response for all the networks is specified using the hyperelastic material model. Any of the hyperelastic models available in Abaqus can be used (see “Hyperelastic behavior of rubberlike materials,” Section 22.5.1). The same hyperelastic material definition is used for all the networks, scaled by a stiffness ratio specific to each network. Consequently, only one hyperelastic material definition is required by the model along with the stiffness ratio for each network. The elastic response can be specified by defining either the instantaneous response or the long-term response.
Viscous behavior must be defined for each viscoelastic network. It is modeled by assuming the multiplicative split of the deformation gradient and the existence of the creep potential, 
, from which the flow rule is derived. In the multiplicative split the deformation gradient is expressed as
is the elastic part of the deformation gradient (representing the hyperelastic behavior) and 
is the creep part of the deformation gradient (representing the stress-free intermediate configuration). The creep potential is assumed to have the general form 
is the Cauchy stress. If the potential is specified, the flow rule can be obtained from 
is the symmetric part of the velocity gradient, 
, expressed in the current configuration and 
is the proportionality factor. In this model the creep potential is given by
, where 
is the equivalent deviatoric Cauchy stress and 
is the equivalent creep stain rate. In this case the flow rule has the form
is the Kirchhoff stress, 
is the determinant of 
, 
is the deviatoric Cauchy stress, 
is the deviatoric Kirchhoff stress, and 
. To complete the derivation, the evolution law for must be provided. In this model can be determined from either a power-law strain hardening model or a hyperborlic-sine model.Only the isotropic thermal expansion is permitted with the nonlinear viscoelastic material (“Thermal expansion,” Section 26.1.2).
The nonlinear viscoelastic response is defined by specifying the identifier, stiffness ratio, and creep law for each viscoelastic network.
Each viscoelastic network in the material model must be assigned a unique network identifier or network id. The network identifiers must be consecutive integers starting with 1. The order in which they are specified is not important.
| Input File Usage: | Use the following option to specify the network identifier: |
*VISCOELASTIC, NONLINEAR, NETWORKID=networkId |
The contribution of each network to the overall response of the material is determined by the value of the stiffness ratio, 
, which is used to scale the elastic response of the network material. The sum of the stiffness ratios of the viscoelastic networks must be smaller than or equal to 1. If the sum of the ratios is equal to 1, the purely elastic equilibrium network is not created. If the sum of the ratios is smaller than 1, the equilibrium network is created with a stiffness ratio, 
, equal to
denotes the number of viscoelastic networks and 
is the stiffness ratio of network 
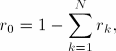
.| Input File Usage: | Use the following option to specify the network's stiffness ratio: |
*VISCOELASTIC, NONLINEAR, SRATIO=ratio |
The definition of creep behavior in Abaqus/Standard is completed by specifying the creep law.
The strain hardening law is defined by specifying three material parameters: A, n, and m. For physically reasonable behavior A and n must be positive and –1 < m ≤ 0.
| Input File Usage: | *VISCOELASTIC, NONLINEAR, LAW=STRAIN |
The hyperbolic sine creep law is specified by providing three nonnegative parameters: A, B, and n.
| Input File Usage: | *VISCOELASTIC, NONLINEAR, LAW=HYPERB |
The material is active during all stress/displacement procedure types. However, the creep effects are taken into account only in a quasi-static analysis (see “Quasi-static analysis,” Section 6.2.5). In other stress/displacement procedures the evolution of the state variables is suppressed and the creep strain remains unchanged.
The nonlinear viscoelastic model is available with continuum elements that include mechanical behavior (elements that have displacement degrees of freedom), except for one-dimensional and plane stress elements.
In addition to the standard output identifiers available in Abaqus/Standard (“Abaqus/Standard output variable identifiers,” Section 4.2.1), the following variables have special meaning for the nonlinear viscoelastic material model:
CEEQ | The overall equivalent creep strain, defined as |
CE | The overall creep strain, defined as |
CENER | The overall viscous dissipated energy per unit volume, defined as |
SENER | The overall elastic strain energy density per unit volume, defined as |
denotes the stiffness ratio for network , denotes the number of viscoelastic networks, the subscript or superscript is used to denote network quantities, and the network 
is assumed to be the purely elastic network.
and 
.
.
.
.